Work out examples much, much more quickly than using pencil & paper!
Test ideas and come up with new theories and conjectures!
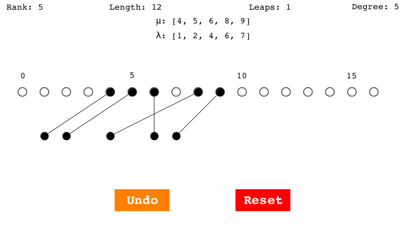
Specifically, Homologica lets you build "allowable functions" f from one weight diagram μ (the top row of dots) to another weight diagram λ (the bottom row of dots). Line segments between the two rows of dots represent the function f.
It turns out that such functions f are in one-to-one correspondence with occurrences of the indecomposable projective module P(λ) in a projective resolution of the (thick) Kac module ∆(μ) of highest weight μ for the periplectic Lie superalgebra p(n). The projective resolution looks like:
⋯ -> P_d -> ⋯ -> P_2 -> P_1 -> P_0 -> ∆(μ) -> 0.
For instructions on the three types of "moves" that are allowed in building f, see http://briandboe.com/homologica.html. Or, just tap dots and explore what is possible and what is not!
For full details and proofs, plus some open questions, see the paper "Complexity and support varieties for type P Lie superalgebras," by Brian D. Boe and Jonathan R. Kujawa, 2020, posted on https://arxiv.org/archive/math (expected availability: late January, 2020).
The fields at the top of the screen are:
Rank: the n of p(n), equal to the number of black dots in each row;
Length: the sum of the μ_i - λ_i, i = 1, 2, ⋯, n;
Leaps: the number of crossings of lines between the two rows of dots;
Degree: the d of P_d in which P(λ) occurs: d = (Length/2) - Leaps;
μ: the positions of the black dots in the top row: [μ_1,⋯, μ_n],
λ: the positions of the black dots in the bottom row: [λ_1,⋯, λ_n].
Features:
Unlimited Undo.
Reset button to clear all black dots and line segments and start over.
Version 1.0. Initial public release.